Savez vous quelle est cette raie d'absorption sur le spectre de Mrk231 ? Si c'est celle du Na elle ne tombe là ou l'on l'attend. Curieux...
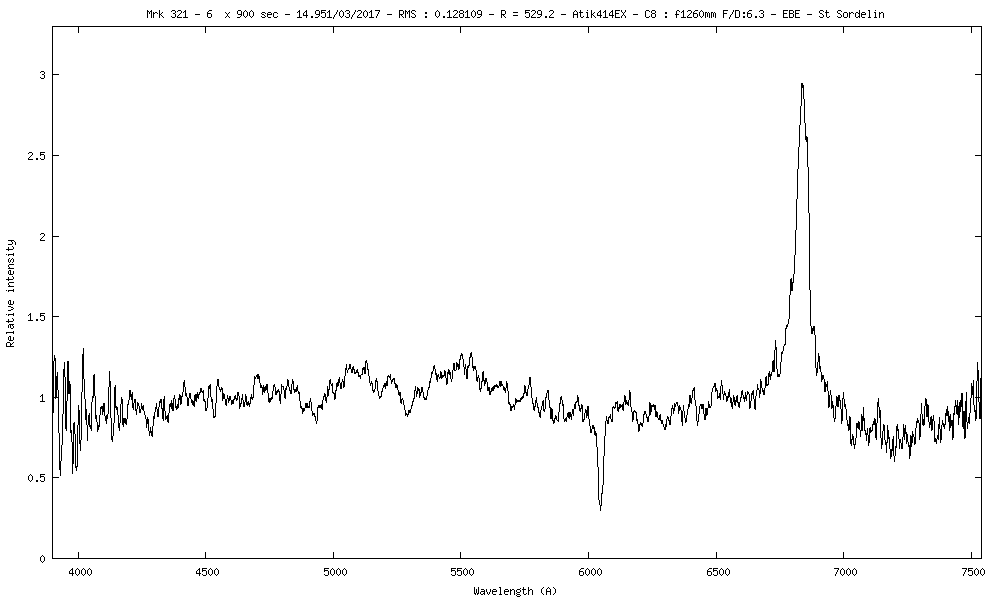
Mrk 231 : Seyfert 1 Galaxy :
Ha est mesurée à 6837A (Ha repos = 6562.8A)
z = 0.04178
Calcul de la vitesse de récession relativiste :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 12 263.12 km/s
d = 175Mpc = 570.5 millions d'années-lumières
La vitesse héliocentrique 24/02/2017 = -4.351 km/s donc la vitesse de récession de Mrk 231 est de 12 258 km/s
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Ha à mi-hauteur (FWHM) en émission. Ha a une largeur de 54A
V = (Delta lambda / lambda) x c
V = (54 / 6562.8) x 299792.458
V = 2467 km/s
---------------------------------------------------------------------------------------
Quasar Twin :



QSO 1247+267 a une vitesse relativiste de récession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 212 108.2 km/s [+/- 50km/s]
Le temps de regard en arrière est de 9.2 millards d'années (voyage de la lumière pour nous parvenir) et l'Univers était agé de 4.5 millards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 13.94 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 1.4162)
a(t) = 0.4138
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~58.6 % ! Maintenant le rayon est plus grand de 1/a(t) = 141.6 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 6.58K
La température de l'Univers était de 6.58K (plus ~2.41 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur des raies en émission à mi-hauteur (FWHM).
CIII] a une largeur de 56A et MgII à une largeur de 90A
Avec la formule V = (Delta lambda / lambda) x c
On trouve des vitesses de 8794km/s et 9643kms, d'ou une moyenne de 9218.5km/s
La vitesse de rotation du disque d'accrétion dans ce Quasar est de 9218.5 km/s.
--------------------------------------------------------------
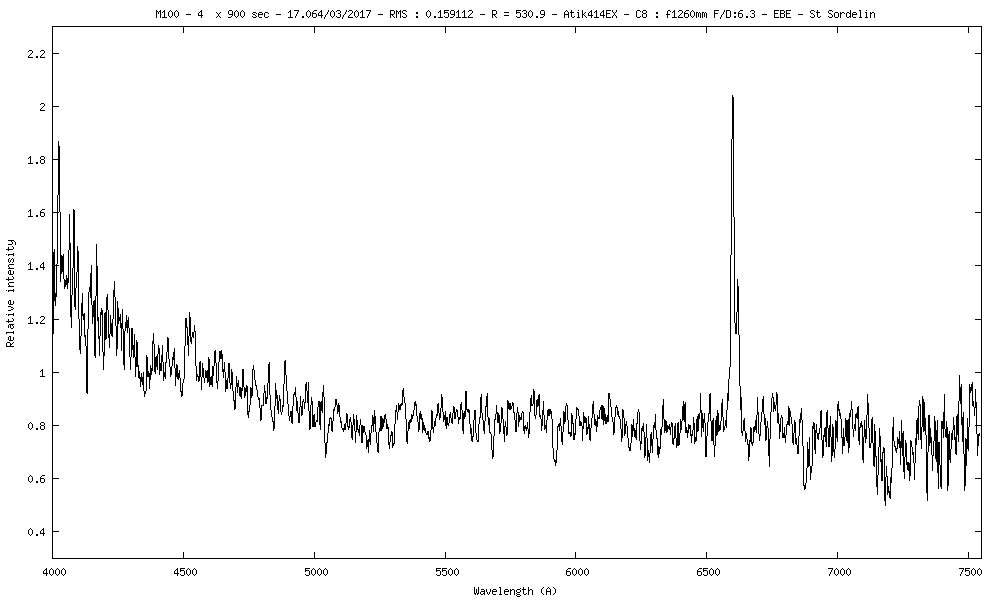
M100 : Active Galaxy Nucleus :
v = 9.35
Ha = 6600A : Ha repos = 6562.8A : z = 0.0056683
[NII] = 6618.5A : [NII] repos = 6584A : z = 0.00523991
moyenne z = 0.0054541
c.z = 1635.1 km/s
d = 23.35Mpc = 76.12 millions d'années-lumières
La vitesse héliocentrique 16/03/2017 = 2.232 km/s donc la vitesse de récession de M100 est de 1637.3 km/s
--------------------------------------------------------------------------
QSO J1701+6412 :

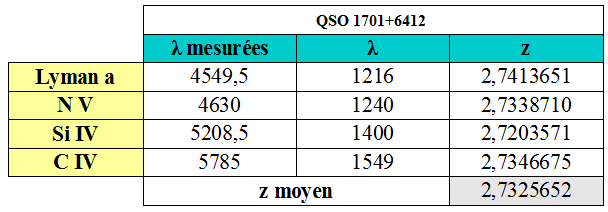
QSO 1247+267 a une vitesse relativiste de récession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 259 636.75 km/s [+/- 50km/s]
Le temps de regard en arrière est de 11.31 milliards d'années (voyage de la lumière pour nous parvenir) et l'Univers était âgé de 2.4 milliards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 20.23 milliards d'années lumières.
Le facteur d'échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.7325)
a(t) = 0.268
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~73.2 % ! Maintenant le rayon est plus grand de 1/a(t) = 273.13 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 10.17K
La température de l'Univers était de 10.17 K (plus ~3.73 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 142A
V = (Delta lambda / lambda) x c
V = (54 / 6562.8) x 299792.458
V = 35 132 km/s
De même Si IV et C IV ont des largeurs de ~95A et ~87A ce qui fait des vitesses de 20 343 km/s et 16 838 km/s.
En moyennant ces largeurs des raies, on trouve une vitesse de rotation du disque d'accrétion de 24 104 km/s.