QSO B0014+810 (ou communément S5 0014+813)
Posted: Fri Dec 02, 2016 12:00 pm
QSO B0014+810 :
(infos Wikipédia)
Vue d'artiste d'un quasar hyper-lumineux semblable à S5 0014+81, entouré d'un disque d'accrétion épais possédant deux jets.

S5 0014+810 (m=16.5) est un quasar ou blazar FSRQ lointain situé dans la constellation de Céphée. Il fait partie d'une galaxie elliptique géante à sursauts de formation d'étoiles.
S5 0014+81 est l'un des quasars les plus lumineux connus et possède l'un des trous noirs les plus massifs jamais recensés, d'une masse estimée à 40 milliards de masses solaires (M☉).
Caractéristiques :
S5 0014+81 est l'un des blazars les plus lumineux connus, dégageant une énergie dépassant les 10^41 watts. Sa magnitude bolométrique absolue est de -31,5 pour une luminosité de 3 846×10^14 fois celle du Soleil, soit l'équivalent de 25000 Voie Lactée !!
Comme les autres blazars, S5 0014+81 possède un trou noir supermassif en son centre qui pourrait être à l'origine de son intense activité.
En 2009, une équipe d'astronome utilisant le télescope spatial SWIFT a déterminé la masse de ce dernier à l'aide de la luminosité bolométrique. Ils ont obtenu une valeur 10 000 fois plus élevée que celle du trou noir situé au centre de la Voie lactée, soit environ 40 milliards de M☉. Cela en fait le trou noir le plus massif connu, plus de six fois plus massif que celui situé au centre de la galaxie elliptique M87, qui a détenu le record pendant 60 ans.
Un tel astre présenterait un rayon de Schwarzschild de 120 milliards de km. L'horizon externe du trou noir présente donc un diamètre de 240 milliards de km,soit environ 1 600 unités astronomiques. Ce diamètre correspond à celui de l'ergosphère. Ce trou noir transformerait l'équivalent de 4 000 M☉ chaque année.
Apparu seulement 1,6 milliards d'années après le Big Bang, il laisse croire que les trous noirs supermassifs sont apparus très rapidement dans l'histoire de l'Univers.
Spectre obtenu assez bruité mais avec de longues :
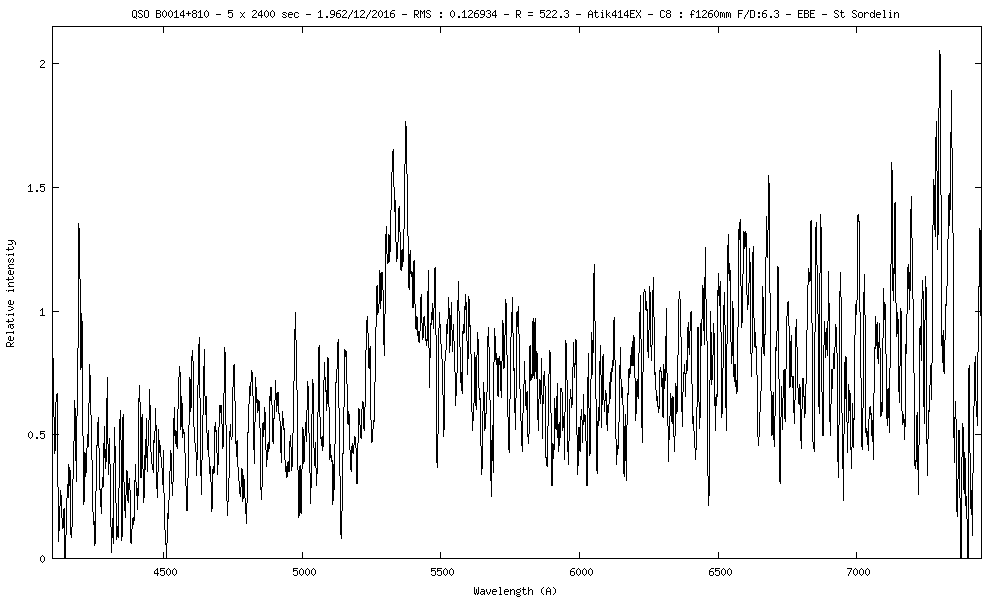
La raie Lyman alpha est une raie très large et asymétrique liée à la diffusion résonnante dans un milieu en expansion. Elle est émise à 1216 angstroms et dans le spectre elle se trouve proche des 5340A.On note à gauche de la raie Lyman a, des encoches dans le spectre correspondant à l'absorption par de petits nuages contenant un peu de gaz le long de la ligne de visée. On appelle cela la forêt de Lyman.
Le fait que la lumière de cette forêt ne soit pas complètement absorbée révèle que le quasar est plus vieux qu' 1 millard d'années, sans quoi cette lumière serait absorbée, alors il n'y aurait pas de signal dans le spectre et il serait plat à cet endroit. Le fait que le signal soit absorbé est l'effet que l'on appelle Gunn-Peterson qui se voit à des quasars de redshift z=6 et qui trahit que l'univers contenait encore beaucoup de gaz neutre à cette époque. Au tour de z=6 soit 1 milliard d'années après le Big Bang, le gaz de l'univers a fini d'être réionisé par la lumière des premières galaxies. La largeur de la dépression de Gunn-Peterson donne une information sur la profondeur en redshift, et donc la durée écoulée depuis l'époque du quasar, pendant laquelle le gaz de l'univers était encore neutre.
(renseignements trouvés dans la partie de Bruno Guiderdon "Les premières galaxies et la fin de l'âge sombre" : livre : "Galaxies et cosmologies" par Françoise Combres, Misha Haywood, Suzy Collin, Florence Durret, Bruno Guiderdoni)
Pour faire les mesures, j'appliques un filtre pour cerner les pics des raies d'émission :
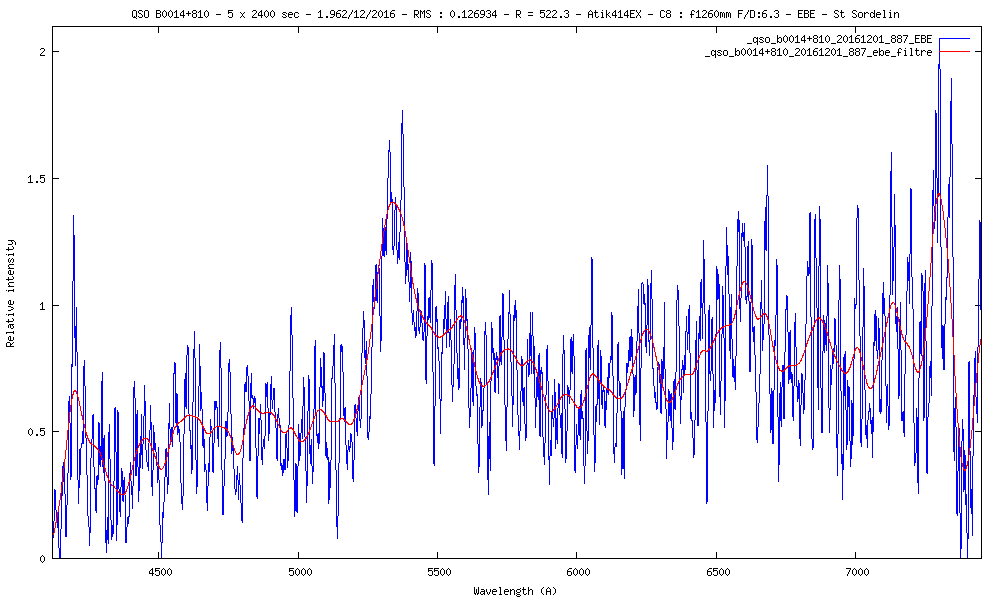
Ce qui donne (sous reserve) :
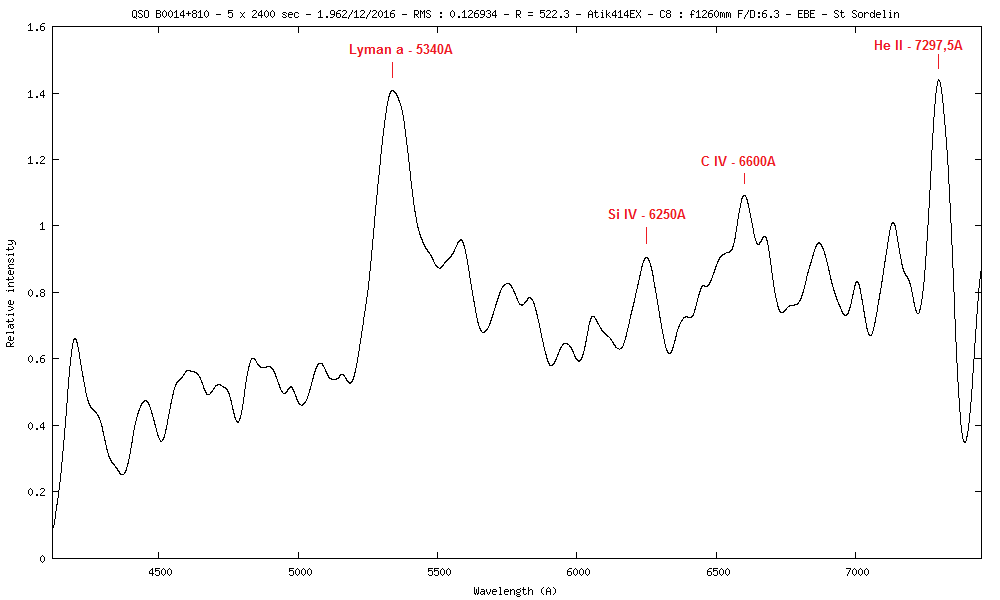
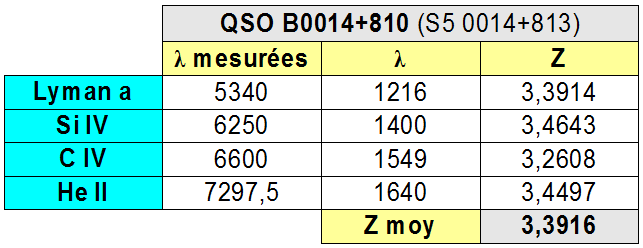
Assez proche des résultats de Simbad qui donne z=3.366
Puis quelques mesures :
:
QSO B0014+810 a une vitesse relativiste de recession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.3916+1)^2 - 1) / ((3.3916 +1)^2 + 1)]
Vr = 299792.458 x (18.286 / 20.286)
Vr = 270 235,9 km/s [+/- 50km/s]
La distance de regard en arrière de 11.83 milliards d'années. Les photons sont partis quand l'Univers avait 1.87 milliards d'années (!!)

Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 22.317 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.3916)
a(t) = 0.2277
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~77.3 % ! Maintenant le rayon est plus grand de 1/a(t) = 339 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
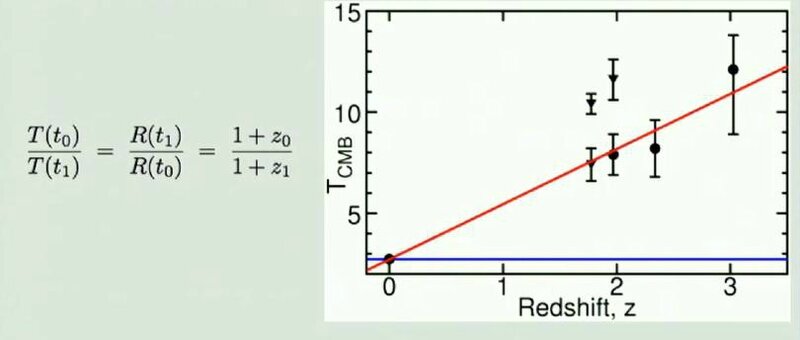
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 3.3916) / (1+0)
T(t1) = 11.96 K
La température de l'Univers était de 11.96 K (plus ~4.4 fois la température actuelle).
(infos Wikipédia)
Vue d'artiste d'un quasar hyper-lumineux semblable à S5 0014+81, entouré d'un disque d'accrétion épais possédant deux jets.

S5 0014+810 (m=16.5) est un quasar ou blazar FSRQ lointain situé dans la constellation de Céphée. Il fait partie d'une galaxie elliptique géante à sursauts de formation d'étoiles.
S5 0014+81 est l'un des quasars les plus lumineux connus et possède l'un des trous noirs les plus massifs jamais recensés, d'une masse estimée à 40 milliards de masses solaires (M☉).
Caractéristiques :
S5 0014+81 est l'un des blazars les plus lumineux connus, dégageant une énergie dépassant les 10^41 watts. Sa magnitude bolométrique absolue est de -31,5 pour une luminosité de 3 846×10^14 fois celle du Soleil, soit l'équivalent de 25000 Voie Lactée !!
Comme les autres blazars, S5 0014+81 possède un trou noir supermassif en son centre qui pourrait être à l'origine de son intense activité.
En 2009, une équipe d'astronome utilisant le télescope spatial SWIFT a déterminé la masse de ce dernier à l'aide de la luminosité bolométrique. Ils ont obtenu une valeur 10 000 fois plus élevée que celle du trou noir situé au centre de la Voie lactée, soit environ 40 milliards de M☉. Cela en fait le trou noir le plus massif connu, plus de six fois plus massif que celui situé au centre de la galaxie elliptique M87, qui a détenu le record pendant 60 ans.
Un tel astre présenterait un rayon de Schwarzschild de 120 milliards de km. L'horizon externe du trou noir présente donc un diamètre de 240 milliards de km,soit environ 1 600 unités astronomiques. Ce diamètre correspond à celui de l'ergosphère. Ce trou noir transformerait l'équivalent de 4 000 M☉ chaque année.
Apparu seulement 1,6 milliards d'années après le Big Bang, il laisse croire que les trous noirs supermassifs sont apparus très rapidement dans l'histoire de l'Univers.
Spectre obtenu assez bruité mais avec de longues :

La raie Lyman alpha est une raie très large et asymétrique liée à la diffusion résonnante dans un milieu en expansion. Elle est émise à 1216 angstroms et dans le spectre elle se trouve proche des 5340A.On note à gauche de la raie Lyman a, des encoches dans le spectre correspondant à l'absorption par de petits nuages contenant un peu de gaz le long de la ligne de visée. On appelle cela la forêt de Lyman.
Le fait que la lumière de cette forêt ne soit pas complètement absorbée révèle que le quasar est plus vieux qu' 1 millard d'années, sans quoi cette lumière serait absorbée, alors il n'y aurait pas de signal dans le spectre et il serait plat à cet endroit. Le fait que le signal soit absorbé est l'effet que l'on appelle Gunn-Peterson qui se voit à des quasars de redshift z=6 et qui trahit que l'univers contenait encore beaucoup de gaz neutre à cette époque. Au tour de z=6 soit 1 milliard d'années après le Big Bang, le gaz de l'univers a fini d'être réionisé par la lumière des premières galaxies. La largeur de la dépression de Gunn-Peterson donne une information sur la profondeur en redshift, et donc la durée écoulée depuis l'époque du quasar, pendant laquelle le gaz de l'univers était encore neutre.
(renseignements trouvés dans la partie de Bruno Guiderdon "Les premières galaxies et la fin de l'âge sombre" : livre : "Galaxies et cosmologies" par Françoise Combres, Misha Haywood, Suzy Collin, Florence Durret, Bruno Guiderdoni)
Pour faire les mesures, j'appliques un filtre pour cerner les pics des raies d'émission :

Ce qui donne (sous reserve) :


Assez proche des résultats de Simbad qui donne z=3.366
Puis quelques mesures
QSO B0014+810 a une vitesse relativiste de recession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.3916+1)^2 - 1) / ((3.3916 +1)^2 + 1)]
Vr = 299792.458 x (18.286 / 20.286)
Vr = 270 235,9 km/s [+/- 50km/s]
La distance de regard en arrière de 11.83 milliards d'années. Les photons sont partis quand l'Univers avait 1.87 milliards d'années (!!)

Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 22.317 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.3916)
a(t) = 0.2277
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~77.3 % ! Maintenant le rayon est plus grand de 1/a(t) = 339 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;

T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 3.3916) / (1+0)
T(t1) = 11.96 K
La température de l'Univers était de 11.96 K (plus ~4.4 fois la température actuelle).